ΚΕΦΑΛΑΙΟ 3
ΠΟΛΙΚΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ
Ένα σημείο
Α στο επίπεδο μπορεί να αναπαρασταθεί κατά μοναδικό τρόπο από δύο αριθμούς (r, θ), όπου r η απόστασή του Α από την αρχή των αξόνων και θΑν το Α έχει καρτεσιανές συντεταγμένες (x, y) και πολικές συντεταγμένες (r, θ), εύκολα βλέπουμε ότι ισχύουν οι παρακάτω σχέσεις
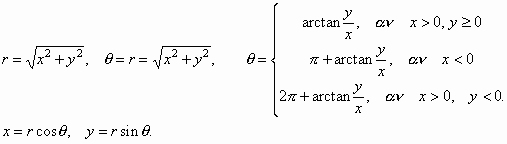
Είναι δυνατόν μια περιοχή
στο επίπεδο να περιγράφεται πιο απλά με την χρήση πολικών συντεταγμένων παρά με την χρήση καρτεσιανών συντεταγμένων. Για παράδειγμα ο δίσκος με κέντρο την αρχή και ακτίνα 1 περιγράφεται από την ανισότητα r £ 1.Θεώρημα: Έστω Π η περιοχή στο xy-επίπεδο που περιγράφεται από τις ανισότητες
a £ θ £ b, c £ r £ d
και Δ το ορθογώνιο παραλληλόγραμμο
που επίσης περιγράφεται από τις παραπάνω ανισότητες αλλά αυτή τη φορά στο rθ-επίπεδο. Έστω f μια φραγμένη συνάρτηση ορισμένη στο Π η οποία είναι συνεχής στο Π εκτός ίσως από ένα πεπερασμένο αριθμό από καμπύλες. Αν f0(r, θ) = f(x, y) = f(rcosθ, rsinθ), τότε η f0 είναι ολοκληρώσιμη στο Δ και![]()
Παρατήρηση
: Το παραπάνω θεώρημα ισχύει και στην περίπτωση περιοχών που περιγράφονται από πιο σύνθετες ανισότητες. Έστω γ, δ δύο συναρτήσεις ορισμένες στο διάστημα [α, β] με 0 £ γ(θ) £ δ(θ). Θεωρούμε την περιοχή Π στο xy-επίπεδο που αποτελείται από τα σημεία των οποίων οι πολικές συντεταγμένες ικανοποιούν τις σχέσειςα
£ θ £ β, 0 £ γ(θ) £ r £ δ(θ).Αν Π
0 είναι η περιοχή στο rθ-επίπεδο που περιγράφουν οι παραπάνω ανισότητες, τότε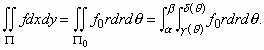
Ασκήσεις
1. Να βρείτε το σύνολο των σημείων στο
xy-επίπεδο που ικανοποιούν την σχέσηr = acosθ, a>0. [Υπόδειξη] [Λύση]
2. Να υπολογίσετε το ολοκλήρωμα της
συνάρτησης f(x, y) = xy2 πάνω στην περιοχή Π που περιγράφεται από τις ανισότητεςx ³ 0, x2 + y2 ³ 1, x2 + y2 £ 4. [Λύση]
3. Να υπολογίσετε το εμβαδόν
της περιοχής που περικλείει η καμπύλη r2 = sinθ. [Λύση]