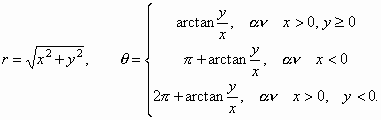
ΚΕΦΑΛΑΙΟ 6
K
ΥΛΙΝΔΡΙΚΕΣ-ΣΦΑΙΡΙΚΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΚΑΙ ΤΡΙΠΛΟ ΟΛΟΚΛΗΡΩΜΑ
Έστω (x, y, z) οι Καρτεσιανές συντεταγμένες ενός σημείου στο χώρο. Για να βρούμε τις κυλινδρικές συντεταγμένες αυτού του σημείου μετατρέπουμε τις δύο πρώτες συντεταγμένες του x, y στις πολικές συντεταγμένες στο xy επίπεδο και αφήνουμε την τρίτη αμετάβλητη. Δηλαδή, αν
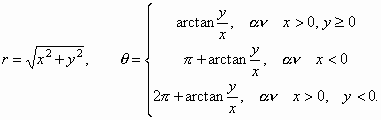
τότε οι κυλινδρικές συντεταγμένες του (x, y, z) είναι οι (r, θ, z).
Θεώρημα 1:
Έστω Α μια περιοχή στο (x, y, z) επίπεδο και Α* η ίδια περιοχή όπως αντιστοιχεί στις κυλινδρικές συντεταγμένες (r, θ, z). Αν η f είναι μια ολοκληρώσιμη συνάρτηση στην Α, τότε η συνάρτηση (r, θ, z) ® f(rcosθ, rsinθ, z) είναι ολοκληρώσιμη στην Α* και![]()
Έστω (x, y, z) οι Καρτεσιανές συντεταγμένες ενός σημείου στο χώρο. Θέτουμε
![]()
και χρησιμοποιούμε πολικές συντεταγμένες στο επίπεδο xy:
x = rcosθ, y = rsinθ
με
![]()
Τότε r = ρsinφ, όπου φ η γωνία μεταξύ του άξονα των z και του διανύσματος (x, y, z). Έτσι
x = ρsinφcosθ, y = ρsinφsinθ, z = ρcosφ
οι οποίες είναι οι σφαιρικές
συντεταγμένες του σημείου (x, y, z).Θεώρημα 2:
Έστω Α μια περιοχή στο (x, y, z) επίπεδο και Α* η ίδια περιοχή όπως αντιστοιχεί στις σφαιρικές συντεταγμένες (ρ, φ, θ). Αν η f είναι μια ολοκληρώσιμη συνάρτηση στην Α, τότε η συνάρτηση (ρ, φ, θ) ® f(ρsinφcosθ, ρsinφsinθ, ρcosφ) είναι ολοκληρώσιμη στην Α* και![]()
Ασκήσεις
1. Να υπολογίσετε τον όγκο της σφαίρας
![]()
χρησιμοποιώντας σφαιρικές συντεταγμένες. [Υπόδειξη] [Λύση]
2. Nα υπολογίσετε το ολοκλήρωμα της συνάρτησης
![]()
πάνω στην περιοχή Α μεταξύ των σφαιρών ακτίνας 1 και ακτίνας a < 1. Ακολούθως να υπολογίσετε το όριο του ολοκληρώματοα καθώς το a πλησιάζει στο 0. [Λύση]
3. Να υπολογισθεί το ολοκλήρωμα της συνάρτησης
f(x, y, z) = y2z στην περιοχή Α η οποία ευρίσκεται μέσα στον κύλινδρο x + y £ 4 και μεταξύ των επιπέδων z = 0 και z = 3. [Λύση]