


Next: Άσκηση 6
Up: Άσκηση 5
Previous: Υπόδειξη
Λύση
Αφού η
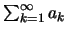 συγκλίνει έχουμε οτι
συγκλίνει έχουμε οτι
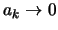 .
Άρα υπάρχει
.
Άρα υπάρχει
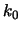 ώστε για κάθε
ώστε για κάθε 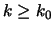 να ισχύει
να ισχύει
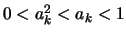 .
Η
.
Η
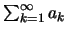 συγκλίνει, οπότε από το κριτήριο σύγκρισης συγκλίνει και η
συγκλίνει, οπότε από το κριτήριο σύγκρισης συγκλίνει και η
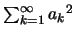 .
.
Για κάθε
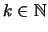 έχουμε
έχουμε
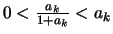 ,
και αφού η
,
και αφού η
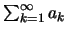 συγκλίνει έπεται οτι και η
συγκλίνει έπεται οτι και η
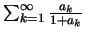 συγκλίνει.
συγκλίνει.
Το ίδιο ισχύει και με την τρίτη σειρά αφού
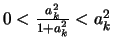 και έχουμε δει
οτι η
και έχουμε δει
οτι η
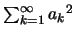 συγκλίνει.
συγκλίνει.
Άσκηση 5
Υπόδειξη
root
1999-07-29
![]() έχουμε
έχουμε
![]() ,
και αφού η
,
και αφού η
![]() συγκλίνει έπεται οτι και η
συγκλίνει έπεται οτι και η
![]() συγκλίνει.
συγκλίνει.
![]() και έχουμε δει
οτι η
και έχουμε δει
οτι η
![]() συγκλίνει.
συγκλίνει.