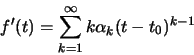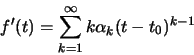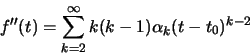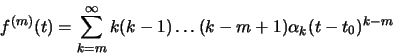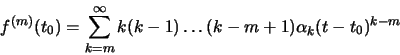Next: Άσκηση 3
Up: Άσκηση 2
Previous: Υπόδειξη
Λύση
Έχουμε δει οτι μια δυναμοσειρά παραγωγίζεται κατά όρους σε οποιοδήποτε σημείο του διαστήματος σύγκλισής της. Δηλαδή, αν
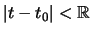 τότε
τότε
Αν θέσουμε 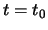 ,
παίρνουμε
,
παίρνουμε
Οι όροι που αντιστοιχούν σε 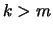 μηδενίζονται, άρα
μηδενίζονται, άρα
Άσκηση 2
Υπόδειξη
root
1999-07-29