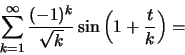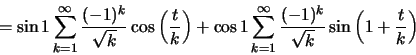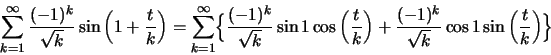
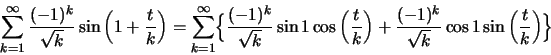
Εξετάζουμε χωριστά τις:
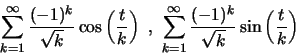
Για την
![]() και η
και η
![]() συγκλίνει, οπότε από το κριτήριο του Weierstrass η
συγκλίνει, οπότε από το κριτήριο του Weierstrass η
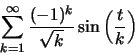
Για την
![]() Η
Η
![]() συγκλίνει, άρα συγκλίνει ομοιόμορφα στο
συγκλίνει, άρα συγκλίνει ομοιόμορφα στο ![]() αν την δούμε σαν σειρά (σταθερών) συναρτήσεων.
Επίσης
αν την δούμε σαν σειρά (σταθερών) συναρτήσεων.
Επίσης
![]() οπότε το κριτήριο του Weierstrass μας δίνει οτι η
οπότε το κριτήριο του Weierstrass μας δίνει οτι η
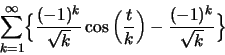
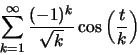
Έπεται οτι η