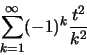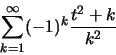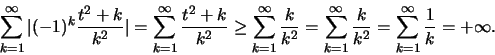Next: Άσκηση 6
Up: Άσκηση 5
Previous: Υπόδειξη
Λύση
Η
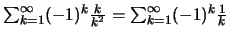 συγκλίνει, ομοιόμορφα στο
συγκλίνει, ομοιόμορφα στο ![$[-A, A]$](img977.gif) αν την δούμε σαν σειρά (σταθερών) συναρτήσεων.
αν την δούμε σαν σειρά (σταθερών) συναρτήσεων.
Αν
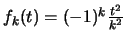 ,
έχουμε
,
έχουμε
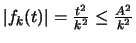 στο
στο ![$[-A, A]$](img977.gif) και η
και η
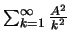 συγκλίνει άρα από το κριτήριο του Weierstrass η
συγκλίνει άρα από το κριτήριο του Weierstrass η
συγκλίνει, ομοιόμορφα στο ![$[-A, A]$](img977.gif) .
Προσθέτοντας, παίρνουμε οτι η
.
Προσθέτοντας, παίρνουμε οτι η
συγκλίνει, ομοιόμορφα στο ![$[-A, A]$](img977.gif) .
.
Είναι:
Άσκηση 705
Υπόδειξη
root
1999-07-29
![]() ,
έχουμε
,
έχουμε
![]() στο
στο ![]() και η
και η
![]() συγκλίνει άρα από το κριτήριο του Weierstrass η
συγκλίνει άρα από το κριτήριο του Weierstrass η