


Next: Άσκηση 4
Up: Άσκηση 3
Previous: Υπόδειξη
Λύση
(α)
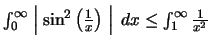 αφού
αφού
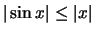 ,
αλλά το δεύτερο ολοκλήρωμα συγκλίνει.
,
αλλά το δεύτερο ολοκλήρωμα συγκλίνει.
(β)
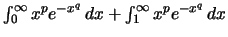 .
Όμως
.
Όμως
και
Παρατηρούμε οτι κάθε φορά που εκτελουμε μια ολοκλήρωση κατά παράγοντες
ο εκθέτης του 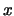 μειώνεται κατά
μειώνεται κατά 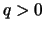 άρα αν επαναλάβουμε τη διαδικασία
άρα αν επαναλάβουμε τη διαδικασία
![$\left[\frac{p}{q}\right] +1$](img1158.gif) φορές θα προκύψει το ολοκλήρωμα:
φορές θα προκύψει το ολοκλήρωμα:
όπου 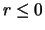 .
Άρα το ολοκλήρωμα συγκλίνει αν και μόνο αν συγκλίνει το
.
Άρα το ολοκλήρωμα συγκλίνει αν και μόνο αν συγκλίνει το
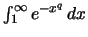 αφού
αφού 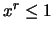 για
για 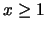 .
Τέλος δείχνουμε οτι το
.
Τέλος δείχνουμε οτι το
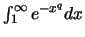 συγκλίνει. Μπορούμε να το δείξουμε με το θεώρημα για τη σύγκλιση σειρών. Το ολοκλήρωμα συγκλίνει αν και μόνο αν συγκλίνει η σειρά
συγκλίνει. Μπορούμε να το δείξουμε με το θεώρημα για τη σύγκλιση σειρών. Το ολοκλήρωμα συγκλίνει αν και μόνο αν συγκλίνει η σειρά
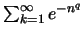 .
Για αυτήν χρησιμοποιούμε το κριτήριο συμπύκνωσης του Cauchy δηλαδή, συγκλίνει αν
και μόνο αν συγκλίνει η
.
Για αυτήν χρησιμοποιούμε το κριτήριο συμπύκνωσης του Cauchy δηλαδή, συγκλίνει αν
και μόνο αν συγκλίνει η
αλλά
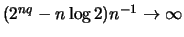 καθώς
καθώς
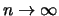 άρα υπάρχει
άρα υπάρχει
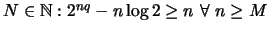 άρα
άρα
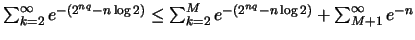 .
Η πρώτη είναι πεπερασμένο
άθροισμα και η δεύτερη γεωμετρική
.
Η πρώτη είναι πεπερασμένο
άθροισμα και η δεύτερη γεωμετρική
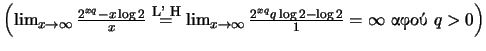 .
.
Άσκηση 3
Υπόδειξη
root
1999-07-29
![]() .
Όμως
.
Όμως
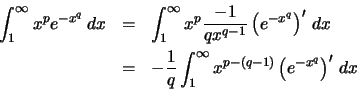
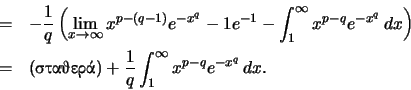
![]() μειώνεται κατά
μειώνεται κατά ![]() άρα αν επαναλάβουμε τη διαδικασία
άρα αν επαναλάβουμε τη διαδικασία
![]() φορές θα προκύψει το ολοκλήρωμα:
φορές θα προκύψει το ολοκλήρωμα:
![\begin{displaymath}(\hbox{μιά άλλη σταθερά}) + \left(\frac1{q}\right)^{1+\left[\frac{p}{q}\right]} \int_1^\infty x^r e^{-x^q} \,dx ,\end{displaymath}](img1159.gif)
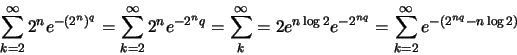
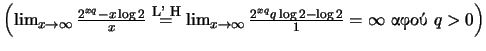 .
.