


Next: Άσκηση 7
Up: Άσκηση 6
Previous: Υπόδειξη
Λύση
Έστω
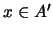 .
Για
.
Για
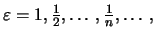 εφαρμόζουμε τον ορισμό και βρίσκουμε
εφαρμόζουμε τον ορισμό και βρίσκουμε
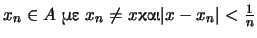 .
Έστω
.
Έστω
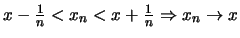 .
Αντίστροφα: Έστω οτι υπάρχουν
.
Αντίστροφα: Έστω οτι υπάρχουν
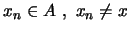 με
με
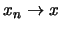 .
Αν μας δώσουν
.
Αν μας δώσουν
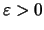 ,
υπάρχει
,
υπάρχει 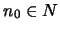 για κάθε
για κάθε 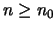 να ισχύει
να ισχύει
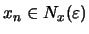 .
Αφού
.
Αφού 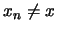 ,
έπεται οτι
,
έπεται οτι
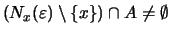 .
Αφού το
.
Αφού το
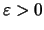 ήταν τυχόν, το
ήταν τυχόν, το 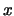 είναι σημείο συσσώρευσης του
είναι σημείο συσσώρευσης του  .
.
Άσκηση 6
Υπόδειξη
root
1999-07-29