


Next: Άσκηση 10
Up: Άσκηση 9
Previous: Υπόδειξη
Λύση
Έστω  μη-κενό, ανοικτό
μη-κενό, ανοικτό
 .
Υπάρχει
.
Υπάρχει 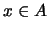 και το
και το 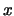 είναι εσωτερικό σημείο του
είναι εσωτερικό σημείο του  ,
άρα υπάρχει
,
άρα υπάρχει
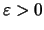 του
του
 .
Ανάμεσα στους
.
Ανάμεσα στους  και
και  μπορούμε να βρούμε και ρητούς και άρρητους αριθμούς. Άρα,
μπορούμε να βρούμε και ρητούς και άρρητους αριθμούς. Άρα,
 και
και
 .
.
Άσκηση 9
Υπόδειξη
root
1999-07-29