


Next: Μετρικοί Χώροι
Up: Άσκηση 11
Previous: Υπόδειξη
Λύση
Αν 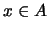 ,
τότε για το
,
τότε για το 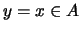 έχουμε
έχουμε
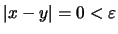 .
Άρα
.
Άρα
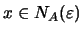 .
Δηλαδή
.
Δηλαδή
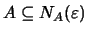 .
Έστω
.
Έστω
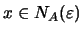 .
Υπάρχει
.
Υπάρχει 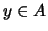 των
των
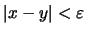 .
Θέτουμε
.
Θέτουμε
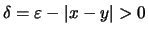 .
Θα δείξουμε οτι
.
Θα δείξουμε οτι
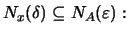 έστω
έστω
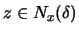 .
Τότε
.
Τότε
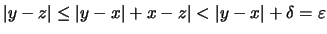 .
Άρα,
.
Άρα,
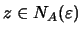 .
Αφού κάθε
.
Αφού κάθε
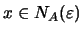 είναι εσωτερικό σημείο του
είναι εσωτερικό σημείο του
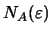 ,
το
,
το
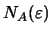 είναι ανοικτό.
Άσκηση 11
Υπόδειξη
είναι ανοικτό.
Άσκηση 11
Υπόδειξη
root
1999-07-29