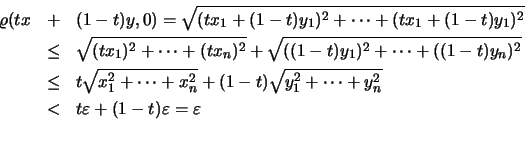
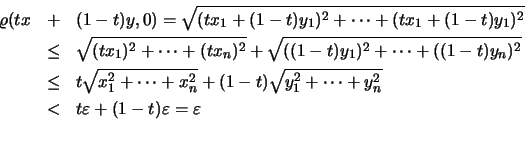
Αν τώρα η ![]() -περιοχή έχει κέντρο οποιδήποτε
-περιοχή έχει κέντρο οποιδήποτε
![]() ,
εύκολα βλέπουμε οτι
,
εύκολα βλέπουμε οτι
![]() αν και μόνο αν
αν και μόνο αν
![]() .
Οπότε, αν
.
Οπότε, αν
![]() και
και ![]() έχουμε:
υπάρχουν
έχουμε:
υπάρχουν
![]() ώστε
ώστε ![]() ,
,
![]() .
Όμως έχουμε δείξει οτι η
.
Όμως έχουμε δείξει οτι η
![]() είναι κυρτή, άρα
είναι κυρτή, άρα
![]() το οποίο δίνει
το οποίο δίνει
![]() .
.
(β) Έστω
![]() και
και ![]() .
Θέλουμε να δείξουμε οτι το
.
Θέλουμε να δείξουμε οτι το ![]() είναι
εσωτερικό σημείο του
είναι
εσωτερικό σημείο του ![]() .
Αφού
.
Αφού
![]() ,
μπορούμε να βρούμε
,
μπορούμε να βρούμε
![]() ώστε
ώστε
![]() .
Θα δείξουμε οτι
.
Θα δείξουμε οτι
![]() .
Έστω
.
Έστω
![]() .
Θεωρούμε το
.
Θεωρούμε το ![]() και το προσθέτουμε στα
και το προσθέτουμε στα ![]() :
αφού
:
αφού
![]() έχουμε
έχουμε
Επίσης,
![]() ,
άρα
,
άρα
![]() .
.