


Next: Υπόδειξη
Up: Στοιχεία Θεωρίας
Previous: Λύση
Άσκηση 4
Ένα υποσύνολο  του
του 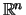 λέγεται κυρτό αν για
λέγεται κυρτό αν για 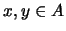 και κάθε
και κάθε
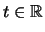 με
με 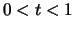 ισχύει οτι
ισχύει οτι
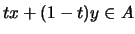 .
Ποιά είναι η γεωμετρική σημασία (στους
.
Ποιά είναι η γεωμετρική σημασία (στους
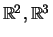 )
αυτού του ορισμού?
Αποδείξτε οτι κάθε
)
αυτού του ορισμού?
Αποδείξτε οτι κάθε 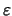 -περιοχή είναι κυρτό σύνολο και ότι, αν
-περιοχή είναι κυρτό σύνολο και ότι, αν  είναι κυρτό, τότε
είναι κυρτό, τότε
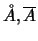 είναι επίσης
κυρτά σύνολα.
Υπόδειξη
Λύση
είναι επίσης
κυρτά σύνολα.
Υπόδειξη
Λύση
root
1999-07-29