


Next: Άσκηση 4
Up: Άσκηση 3
Previous: Υπόδειξη
Λύση
(α) Οι τρεις πρώτες ιδιότητες της μετρικής ελέγχονται εύκολα για την 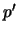 .
Δείχνουμε την τριγωνική ιδιότητα: Έστω
.
Δείχνουμε την τριγωνική ιδιότητα: Έστω 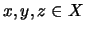 .
Τότε,
.
Τότε,
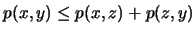 .
Η συνάρτηση
.
Η συνάρτηση
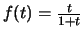 είναι αύξουσα στο
είναι αύξουσα στο 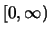 ,
άρα
,
άρα
(β) Αφού
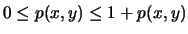 ,
είναι φανερό οτι
,
είναι φανερό οτι
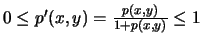 .
.
(γ) Θέτουμε
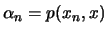 .
Τότε
.
Τότε
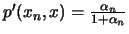 .
Αν
.
Αν
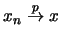 τότε
τότε
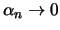 και
και
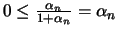 .
Άρα,
.
Άρα,
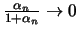 δηλαδή
δηλαδή
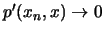 δηλαδή
δηλαδή
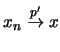 .
Αντίστροφα, αν
.
Αντίστροφα, αν
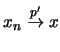 έχουμε
έχουμε
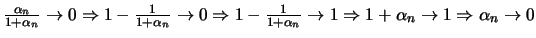 δηλαδή
δηλαδή
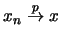 .
.
(δ) Έστω
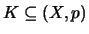 κλειστό. Θα δείξουμε οτι είναι κλειστό και ως προς την
κλειστό. Θα δείξουμε οτι είναι κλειστό και ως προς την 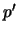 :
αν
:
αν 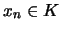 και
και
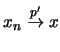 ,
τότε
,
τότε
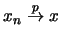 (από το (
(από το (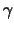 )), και αφού το
)), και αφού το 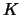 είναι κλειστό ως προς την
είναι κλειστό ως προς την 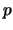 έχουμε
έχουμε 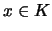 .
Αφού η
.
Αφού η 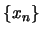 ήταν τυχούσα
ήταν τυχούσα 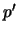 - συγκλίνουσα ακολουθία στο
- συγκλίνουσα ακολουθία στο 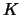 ,
το
,
το 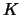 είναι
είναι 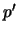 -κλειστό.
Όμοια δείχνουμε οτι κάθε
-κλειστό.
Όμοια δείχνουμε οτι κάθε 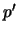 -κλειστό σύνολο είναι και
-κλειστό σύνολο είναι και 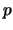 -κλειστό.
-κλειστό.
Άσκηση 3
Υπόδειξη
root
1999-07-29
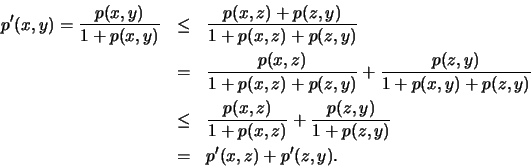
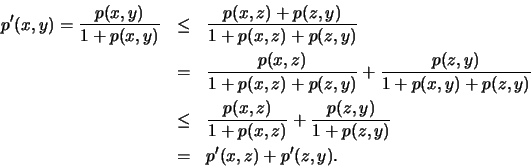
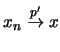 .
Αντίστροφα, αν
.
Αντίστροφα, αν
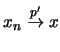 έχουμε
έχουμε
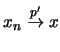 ,
τότε
,
τότε