


Next: Υπόδειξη
Up: Στοιχεία Θεωρίας
Previous: Λύση
Άσκηση 3
Αν 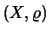 είναι μετρικός χώρος και ορίσουμε:
είναι μετρικός χώρος και ορίσουμε:
τότε
(α) η
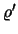 είναι μετρική στον
είναι μετρική στον 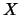
(β)
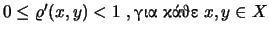
(γ)
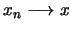 στον
στον
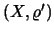 αν και μόνον αν
αν και μόνον αν
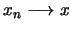 στον
στον 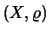 .
.
(δ) τα κλειστά σύνολα στον
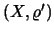 είναι τα ίδια με τα κλειστά σύνολα
στον
είναι τα ίδια με τα κλειστά σύνολα
στον 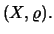 Υπόδειξη
Λύση
Υπόδειξη
Λύση
root
1999-07-29