


Next: Άσκηση 2
Up: Άσκηση 1
Previous: Υπόδειξη
Λύση
(α) Τα διαστήματα της μορφής ![$[a, b]$](img20.gif) είναι κλειστά, τα
είναι κλειστά, τα 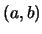 ανοιχτά και τα
ανοιχτά και τα ![$(s,b]$](img53.gif) ή
ή
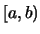 τίποτα. Όλα αυτά έχουν εσωτερικό το
τίποτα. Όλα αυτά έχουν εσωτερικό το 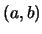 ,
θήκη το
,
θήκη το ![$[a, b]$](img20.gif) ,
σύνορο το
,
σύνορο το 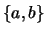 και
σύνολο σημείων συσσώρευσης το
και
σύνολο σημείων συσσώρευσης το ![$[a, b]$](img20.gif) .
.
(β) Τα σύνολα με πεπερασμένο πλήθος στοιχείων στο 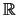 είναι κλειστά,
έχουν κενό εσωτερικό, ταυτίζονται με τη θήκη τους και με το σύνορό τους και δεν
έχουν σημεία συσσώρευσης.
είναι κλειστά,
έχουν κενό εσωτερικό, ταυτίζονται με τη θήκη τους και με το σύνορό τους και δεν
έχουν σημεία συσσώρευσης.
(γ) Ισχύουν τα ίδια με το (β).
(δ) Το 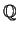 δεν είναι ούτε ανοιχτό ούτε κλειστό. Έχει κενό εσωτερικό,
θήκη, σύνορο και σύνολο σημείων συσσώρευσης όλο το
δεν είναι ούτε ανοιχτό ούτε κλειστό. Έχει κενό εσωτερικό,
θήκη, σύνορο και σύνολο σημείων συσσώρευσης όλο το 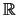 .
.
(ε) Το σύνολο αυτό έχει κενό εσωτερικό, θήκη και σύνορο τον εαυτό του ένωση με το 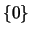 ,
και σημεία συσσώρευσης το
,
και σημεία συσσώρευσης το 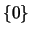 .
.
(στ) Το σύνολο αυτό έχει κενό εσωτερικό, θήκη και σύνορο τον εαυτό του ένωση με το 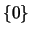 ,
και σημεία συσσώρευσης το
,
και σημεία συσσώρευσης το
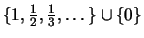 ,
,
Ομοίως κάνουμε και τα υπόλοιπα.
Άσκηση 1
Υπόδειξη
root
1999-07-29