


Next: Άσκηση 4
Up: Άσκηση 3
Previous: Υπόδειξη
Λύση
(α) Σταθεροποιούμε κάποιο 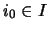 .
Κάθε
.
Κάθε 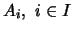 είναι κλειστό σύνολο
(τα συμπαγή είναι κλειστά), άρα το
είναι κλειστό σύνολο
(τα συμπαγή είναι κλειστά), άρα το
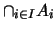 είναι κλειστό.
είναι κλειστό.
Επίσης,
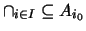 και το
και το 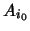 είναι συμπαγές. Άρα το
είναι συμπαγές. Άρα το
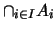 είναι συμπαγές.
είναι συμπαγές.
(β) Έστω
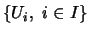 μία ανοιχτή κάλυψη του
μία ανοιχτή κάλυψη του
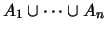 .
Έχουμε
.
Έχουμε
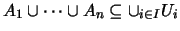 ,
άρα και
,
άρα και
Δηλαδή τα 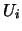 σχηματίζουν ανοιχτή κάλυψη για καθένα από τα
σχηματίζουν ανοιχτή κάλυψη για καθένα από τα 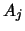 .
Το
.
Το 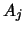 είναι συμπαγές άρα υπάρχει πεπερασμένη υποκάλυψη: μπορούμε να βρούμε
είναι συμπαγές άρα υπάρχει πεπερασμένη υποκάλυψη: μπορούμε να βρούμε
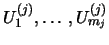 από την κάλυψη ώστε
από την κάλυψη ώστε
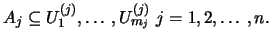 Τότε,
Τότε,
δηλαδή βρήκαμε πεπερασμένη υποκάλυψη για το
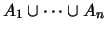 .
Άρα το
.
Άρα το
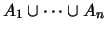 είναι συμπαγές.
είναι συμπαγές.
(γ) Θετουμε 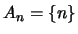 για
για 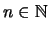 .
Κάθε
.
Κάθε 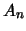 είναι συμπαγές
όμως το
είναι συμπαγές
όμως το
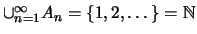 δεν είναι
συμπαγές αφού δεν είναι φραγμένο.
δεν είναι
συμπαγές αφού δεν είναι φραγμένο.
Άσκηση 3
Υπόδειξη
root
1999-07-29
![]() .
Κάθε
.
Κάθε ![]() είναι κλειστό σύνολο
(τα συμπαγή είναι κλειστά), άρα το
είναι κλειστό σύνολο
(τα συμπαγή είναι κλειστά), άρα το
![]() είναι κλειστό.
είναι κλειστό.
![]() και το
και το ![]() είναι συμπαγές. Άρα το
είναι συμπαγές. Άρα το
![]() είναι συμπαγές.
είναι συμπαγές.
![]() μία ανοιχτή κάλυψη του
μία ανοιχτή κάλυψη του
![]() .
Έχουμε
.
Έχουμε
![]() ,
άρα και
,
άρα και