


Next: Υπόδειξη
Up: Συμπάγεια
Previous: Λύση
Άσκηση 3
Έστω μετρικός χώρος 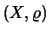 και
και
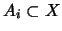
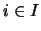 .
(α) Αν τα
.
(α) Αν τα 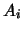 είναι συμπαγή τότε το
είναι συμπαγή τότε το
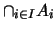 είναι συμπαγές.
είναι συμπαγές.
(β) Αν τα 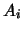 είναι συμπαγή και πεπερασμένου πλήθους (το
είναι συμπαγή και πεπερασμένου πλήθους (το 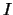 είναι πεπερασμένο)
τότε το
είναι πεπερασμένο)
τότε το
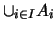 είναι συμπαγές.
Βρείτε στον
είναι συμπαγές.
Βρείτε στον 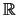 άπειρου πλήθους υποσύνολα
άπειρου πλήθους υποσύνολα
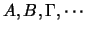 συμπαγή ώστε το
συμπαγή ώστε το
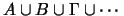 να μην είναι
συμπαγές.
Υπόδειξη
Λύση
να μην είναι
συμπαγές.
Υπόδειξη
Λύση
root
1999-07-29