


Next: Άσκηση 3
Up: Άσκηση 2
Previous: Υπόδειξη
Λύση
Ψάχνουμε θετικό αριθμό 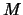 με την ιδιότητα
με την ιδιότητα 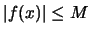 για κάθε
για κάθε 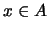 .
To
.
To  είναι φραγμένο, επομένως περιέχεται σε κάποιο διάστημα: έστω οτι
είναι φραγμένο, επομένως περιέχεται σε κάποιο διάστημα: έστω οτι
H 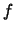 είναι ομοιόμορφα συνεχής στο
είναι ομοιόμορφα συνεχής στο  ,
άρα για
,
άρα για
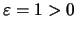 μπορούμε να βρούμε
μπορούμε να βρούμε 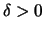 που αν
που αν 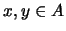 και
και 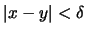 τότε
τότε 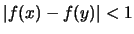 .
Βρίσκουμε
.
Βρίσκουμε
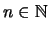 αρκετά μεγάλο ώστε
αρκετά μεγάλο ώστε
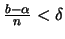 και χωρίζουμε το
και χωρίζουμε το ![$[\alpha , b]$](img379.gif) σε
σε 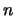 ίσα υποδιαστήματα
ίσα υποδιαστήματα
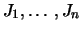 μήκους
μήκους
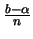 .
Από αυτά τα διαστήματα κρατάμε μόνο εκείνα που έχουν μη κενή τομή με το
.
Από αυτά τα διαστήματα κρατάμε μόνο εκείνα που έχουν μη κενή τομή με το  :
έστω
:
έστω
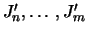 εκείνα τα
εκείνα τα 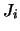 για τα οποία
για τα οποία
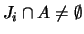 .
Σε κάθε
.
Σε κάθε
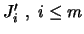 επιλέγουμε τυχόν
επιλέγουμε τυχόν
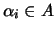 .
Έχουμε δηλαδή
.
Έχουμε δηλαδή
Θα δείξουμε οτι
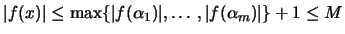 Έστω
Έστω 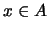 .
Υπάρχει
.
Υπάρχει 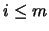 του
του
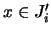 και τότε
και τότε
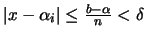 ,
οπότε
,
οπότε
Άσκηση 2
Υπόδειξη
root
1999-07-29