


Next: Άσκηση 6
Up: Άσκηση 5
Previous: Υπόδειξη
Λύση
Χρησιμοποιούμε την απαγωγή σε άτοπο. Έστω οτι
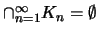 .
Τότε
.
Τότε
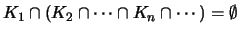 ,
δηλαδή:
,
δηλαδή:
Κάθε 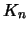 είναι συμπαγές άρα και κλειστό. Επομένως τα
είναι συμπαγές άρα και κλειστό. Επομένως τα
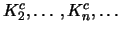 είναι
ανοιχτά και αποτελούν κάλυψη του
είναι
ανοιχτά και αποτελούν κάλυψη του 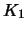 .
Αφού το
.
Αφού το 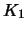 είναι συμπαγές, υπάρχει
πεπερασμένη υποκάλυψη. Υπάρχουν δηλαδή
είναι συμπαγές, υπάρχει
πεπερασμένη υποκάλυψη. Υπάρχουν δηλαδή
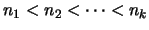 ώστε
ώστε
Άρα
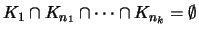 .
Όμως τα
.
Όμως τα 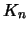 είναι
εγκιβωτισμένα, άρα
είναι
εγκιβωτισμένα, άρα
Οπότε
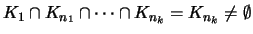 ,
άτοπο.
,
άτοπο.
Άσκηση 5
Υπόδειξη
root
1999-07-29