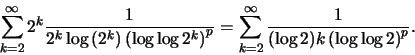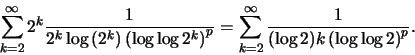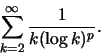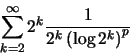Λύση

Εφαρμόζουμε το κριτήριο συμπύκνωσης του Cauchy: κοιτάμε δηλαδή αν συγκλίνει η σειρά:

$$\sum_{k=2}^\infty 2^k \frac1{2^k \log \left( 2^k \right) \lef... ...sum_{k=2}^\infty \frac1{(\log 2) k\left( \log\log 2\right)^p} .$$

Αρκεί να δούμε λοιπόν αν συγκλίνει η

$$\sum_{k=2}^\infty \frac1{k(\log k)^p} .$$

Για αυτήν τώρα ξαναχρησιμοποιούμε το κριτήριο συμπύκνωσης, δηλαδή συγκλίνει αν και μόνο αν συγκλίνει η

$$\sum_{k=2}^\infty 2^k \frac1{2^k \left(\log 2^k \right)^p}$$

η οποία συγκλίνει αν και μόνο αν συγκλίνει η

$$\sum_{k=2}^\infty \frac1{k^p}$$

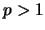η οποία συγκλίνει αν και μόνο αν $p>1$. Το ίδιο λοιπόν ισχύει και για τη δοθείσα σειρά.

Άσκηση 1 Υπόδειξη