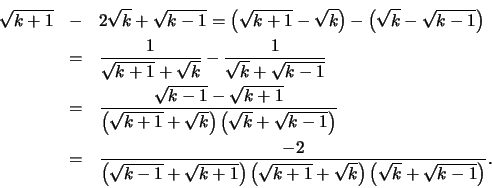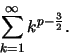(α) Αν ![]() ,
τότε
,
τότε
![]() ,
οπότε η σειρά αποκλίνει. Αν
,
οπότε η σειρά αποκλίνει. Αν ![]() ,
πάλι
,
πάλι
![]() για μεγάλα
για μεγάλα ![]() οπότε
οπότε
![]() και αφού η
και αφού η
![]() αποκλίνει το ίδιο θα ισχύει για την
αποκλίνει το ίδιο θα ισχύει για την
![]() .
.
(β) Αν ![]() ,
τότε εφαρμόζουμε κριτήριο του λόγου:
,
τότε εφαρμόζουμε κριτήριο του λόγου:
![]() ,
άρα η σειρά συγκλίνει.
Αν
,
άρα η σειρά συγκλίνει.
Αν ![]() ,
τότε
,
τότε
![]() ,
άρα η σειρά αποκλίνει.
,
άρα η σειρά αποκλίνει.
(γ) Είναι
![]() τότε η
τότε η
![]() αποκλίνει άρα και η
αποκλίνει άρα και η
![]() .
Αν
.
Αν ![]() ,
τότε
,
τότε
![]() για μεγάλα
για μεγάλα ![]() ,
δηλαδή
,
δηλαδή
![]() και αφού η
και αφού η
![]() συγκλίνει,
το ίδιο ισχύει για την
συγκλίνει,
το ίδιο ισχύει για την
![]() (κριτήριο σύγκρισης).
(κριτήριο σύγκρισης).
(δ) Έχουμε
![]() (αφού
(αφού
![]() είναι φραγμένη). Άρα
είναι φραγμένη). Άρα
![]() και αφού η
και αφού η
![]() αποκλίνει το ίδιο ισχύει για την
αποκλίνει το ίδιο ισχύει για την
![]() .
.
(ε) Είναι
![]() .
Αν
.
Αν ![]() ,
τότε η
,
τότε η
![]() αποκλίνει, άρα και η
αποκλίνει, άρα και η
![]() .
Έστω
.
Έστω ![]() .
Είναι
.
Είναι
![]() αν
αν ![]() δηλαδή
δηλαδή
![]() .
Δηλαδή τελικά
.
Δηλαδή τελικά
![]() .
Όμως, η
.
Όμως, η
![]() συγκλίνει, άρα και η
συγκλίνει, άρα και η
![]() (κριτήριο σύγκρισης).
(κριτήριο σύγκρισης).
(στ) Είναι
![]() .
Άρα,
.
Άρα,
![]() και η σειρά αποκλίνει (πάρτε
και η σειρά αποκλίνει (πάρτε ![]() ).
).
(ζ) Είναι ![]() αν
αν ![]() .
Άρα
.
Άρα
![]() για μεγάλα
για μεγάλα ![]() .
Αφού η
.
Αφού η
![]() συγκλίνει, θα συγκλίνει και η
συγκλίνει, θα συγκλίνει και η
![]() .
.
(η) Η ακολουθία είναι φθίνουσα με θετικούς όρους, οπότε μπορούμε να εφαρμόσουμε το κριτήριο συμπύκνωσης του Cauchy: Θεωρούμε την
![]() .
.
Έχουμε:
![]()
![]() .
για μεγάλα
.
για μεγάλα ![]() (γιατί?) Άρα,
(γιατί?) Άρα,
![]() οπότε η
οπότε η ![]() αποκλίνει και το ίδιο ισχύει για την (η).
αποκλίνει και το ίδιο ισχύει για την (η).
(θ) Έχουμε
![]() .
Άρα, η
.
Άρα, η
(ι) Είναι: