


Next: Άσκηση 41
Up: Eρμιτιανές και Συμμετρικές απεικονίσεις
Previous: Eρμιτιανές και Συμμετρικές απεικονίσεις
Πρόταση 7
Αν

είναι διανυσματικός χώρος με εσωτερικό γινόμενο και
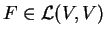
τότε υπάρχει
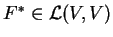
ώστε
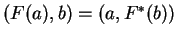
για κάθε
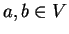
.
H απεικόνιση
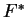
λέγεται δυϊκή της
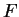
.
Αν
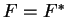
τότε η
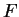
λέγεται
αυτοδυϊκή.
Θεώρημα 22
Μια γραμμική απεικόνιση
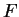
είναι αυτοδυϊκή αν και μόνο αν ο πίνακας της
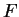
ως προς μια ορθοκανονική βάση, έστω

,
είναι ερμιτιανός
(
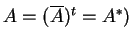
.
Πόρισμα 6
Οι ιδιοτιμές μιας αυτοδυϊκής απεικόνισης είναι πραγματικές.
Πρόταση 8
Δύο ιδιοδιανύσματα που αντιστοιχούν σε διαφορετικές ιδιοτιμές μιας
αυτοδυϊκής απεικόνισης είναι κάθετα μεταξύ τους.
Λήμμα 1
Αν
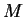
είναι αναλλοίωτος υπόχωρος του διανυσματικού χώρου

ως πρός μια
αυτοδυϊκή απεικόνιση
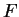
,
τότε ο
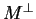
είναι αναλλοίωτος
ως προς
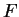
.
Θεώρημα 23 (Φασματικό Θεώρημα)
Αν
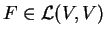
μια αυτοδυϊκή απεικόνιση του

,
τότε ο

έχει μια ορθοκανονική βάση που αποτελείται από ιδιοδιανύσματα της
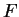
.
Vassilis Metaftsis
1999-09-15