


Next: Ισομετρίες - Ορθογώνιες απεικονίσεις
Up: Άσκηση 43
Previous: Υπόδειξη
Αν η 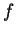 είναι αυτοδυϊκή τότε
είναι αυτοδυϊκή τότε
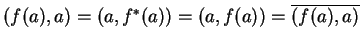 άρα το
άρα το
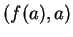 είναι πραγματικός αριθμός.
είναι πραγματικός αριθμός.
Αντίστροφα, αν
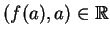 για κάθε
για κάθε 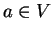 τότε
τότε
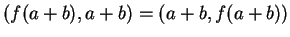 η οποία δίνει ισοδύναμα
η οποία δίνει ισοδύναμα
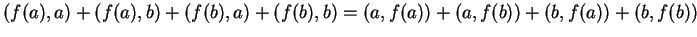 .
Αλλά
.
Αλλά
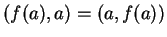 και
και
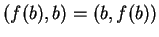 τότε
τότε
Η 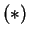 ισχύει για κάθε
ισχύει για κάθε 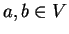 .
Στην θέση του
.
Στην θέση του 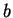 θέτω
θέτω 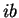 .
Τότε η
.
Τότε η
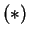 γίνεται
γίνεται
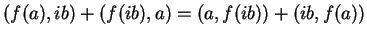 η οποία
ισοδύναμα δίνει
η οποία
ισοδύναμα δίνει
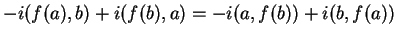 δηλαδή
δηλαδή
Αν
προσθέσω τις 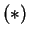 και
και 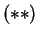 κατά μέλη παίρνω
κατά μέλη παίρνω
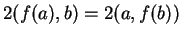 ή ισοδύναμα
ή ισοδύναμα
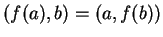 .
Άρα
.
Άρα
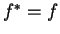 .
.
Vassilis Metaftsis
1999-09-15
![]() για κάθε
για κάθε ![]() τότε
τότε
![]() η οποία δίνει ισοδύναμα
η οποία δίνει ισοδύναμα
![]() .
Αλλά
.
Αλλά
![]() και
και
![]() τότε
τότε