


Next: Άσκηση 11
Up: Άσκηση 10
Previous: Υπόδειξη
Υποθέτουμε ότι η ιδιοτιμή 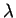 αντιστοιχεί στο ιδιοδιάνυσμα
αντιστοιχεί στο ιδιοδιάνυσμα 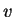 .
Aπό τον ορισμό ξέρουμε ότι
.
Aπό τον ορισμό ξέρουμε ότι
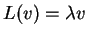 .
Άρα,
.
Άρα,
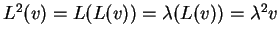 και γενικά
και γενικά
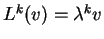 για κάθε
για κάθε
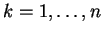 .
Επομένως, αν
.
Επομένως, αν
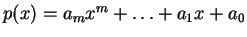 τότε
τότε
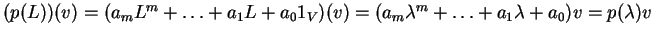 το οποίο σημαίνει ότι το
το οποίο σημαίνει ότι το 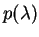 είναι μια
ιδιοτιμή του
είναι μια
ιδιοτιμή του 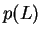 .
.
Vassilis Metaftsis
1999-09-15