


Next: Διαγωνοποιήσιμοι Πίνακες
Up: Άσκηση 12
Previous: Υπόδειξη
Έστω 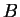 και
και 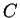 στοιχεία του
στοιχεία του  .
Τότε
.
Τότε
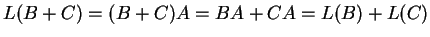 .
Eπίσης,
.
Eπίσης,
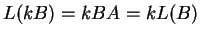 και άρα
η
και άρα
η 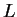 γραμμική. Έχουμε επίσης ότι
γραμμική. Έχουμε επίσης ότι
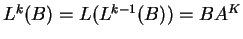 (με
την βοήθεια της επαγωγής) για κάθε
(με
την βοήθεια της επαγωγής) για κάθε 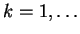 .
Έστω τώρα
.
Έστω τώρα 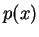 ένα πολυώνυμο με συντελεστές στο
ένα πολυώνυμο με συντελεστές στο 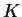 .
Tότε
.
Tότε 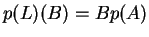 και άρα
και άρα
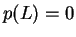 αν και μόνο αν
αν και μόνο αν 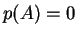 .
Άρα τα
.
Άρα τα 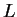 και
και  έχουν τα ίδια
ελάχιστα πολυώνυμα. Αντίθετα, για τα χαρακτηριστικά πολυώνυμα
παρατηρούμε ότι το χαρακτηριστικό πολυώνυμο του
έχουν τα ίδια
ελάχιστα πολυώνυμα. Αντίθετα, για τα χαρακτηριστικά πολυώνυμα
παρατηρούμε ότι το χαρακτηριστικό πολυώνυμο του  είναι βαθμού
είναι βαθμού
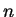 ενώ αυτό της
ενώ αυτό της 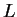 είναι βαθμού
είναι βαθμού 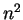 .
.
Vassilis Metaftsis
1999-09-15