


Next: Άσκηση 20
Up: Τριγωνοποίηση
Previous: Τριγωνοποίηση
Ορισμός 6
Ένας πίνακας καλείται άνω τριγωνικός (κάτω τριγωνικός) αν τα στοιχεία
του που βρίσκονται κάτω (πάνω) από την κύρια διαγώνιο είναι μηδενικά.
Πρόταση 4
Oι ιδιοτιμές ενός τριγωνικού πίνακα είναι ακριβώς τα στοιχεία
της κυρίας διαγωνίου. Το χαρακτηριστικό, όπως και το ελάχιστο
πολυώνυμο, είναι γινόμενο πρωτοβάθμιων παραγόντων.
Ορισμός 7
Mια γραμμική απεικόνιση της οποίας ο πίνακας ως προς μια βάση είναι
τριγωνικός λέγεται τριγωνοποιήσιμη. Ένας πίνακας λέγεται τριγωνοποιήσιμος
αν είναι όμοιος με έναν τριγωνικό πίνακα.
Θεώρημα 13
Mια γραμμική απεικόνιση είναι τριγωνοποιήσιμη αν και μόνο αν το
χαρακτηριστικό πολυώνυμο είναι γινόμενο πρωτοβάθμιων παραγόντων.
Πόρισμα 2
Αν

είναι ένας
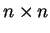
πίνακας με στοιχεία στο σώμα
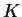
και
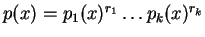
η ανάλυση του ελαχίστου πολυωνύμου, όπου τα
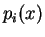
είναι πολυώνυμα
ανάγωγα στο
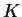
τότε ο

είναι όμοιος με ένα πίνακα της μορφής
όπου ο πίνακας
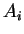
έχει στοιχεία στο
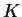
και ο
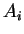
έχει
ελάχιστο πολυώνυμο το
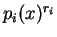
.
Vassilis Metaftsis
1999-09-15
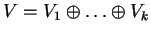
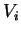 είναι αναλλοίωτος ως προς
είναι αναλλοίωτος ως προς 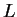 .
.
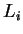 είναι ο περιορισμός της
είναι ο περιορισμός της 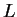 στο
στο 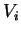 τότε το ελάχιστο
πολυώνυμο της
τότε το ελάχιστο
πολυώνυμο της 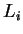 είναι το
είναι το 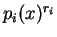 .
.
