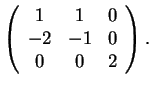Next: Ρητή μορφή και κανονική
Up: Άσκηση 20
Previous: Υπόδειξη
Το χαρακτηριστικό πολυώνυμο της  είναι
είναι
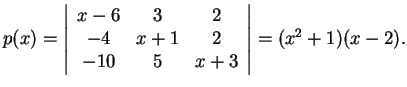 Θέτω
Θέτω
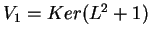 και
και 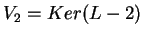 .
Στην
.
Στην 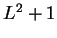 αντιστοιχεί ο
πίνακας
αντιστοιχεί ο
πίνακας
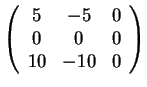 από τον οποία βρίσκω ότι το
από τον οποία βρίσκω ότι το 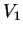 παράγεται από
τα διανύσματα
παράγεται από
τα διανύσματα 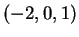 και
και 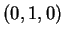 .
Στον
.
Στον 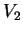 αντιστοιχεί ο πίνακας
αντιστοιχεί ο πίνακας
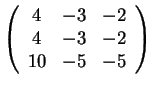 από τον οποία βρίσκω ότι το
από τον οποία βρίσκω ότι το 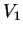 παράγεται από
το διάνυσμα
παράγεται από
το διάνυσμα 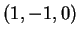 .
Άρα, ως προς την βάση
.
Άρα, ως προς την βάση
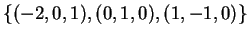 ο
ο  είναι όμοιος με τον πίνακα
είναι όμοιος με τον πίνακα
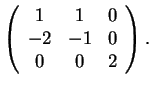
Vassilis Metaftsis
1999-09-15
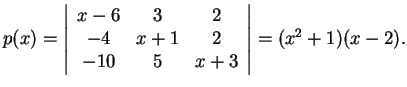 Θέτω
Θέτω
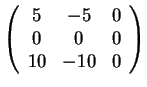 από τον οποία βρίσκω ότι το
από τον οποία βρίσκω ότι το 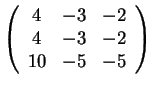 από τον οποία βρίσκω ότι το
από τον οποία βρίσκω ότι το