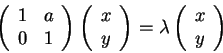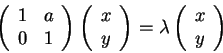Next: Άσκηση 3
Up: Άσκηση 2
Previous: Υπόδειξη
Έστω 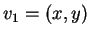 ένα ιδιοδιάνυσμα του
ένα ιδιοδιάνυσμα του  .
Tότε
.
Tότε
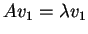 ή
ισοδύναμα
ή
ισοδύναμα
από το οποίο παίρνω τις εξισώσεις
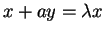 ,
,
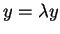 .
Η λύση των παραπάνω δίνει
.
Η λύση των παραπάνω δίνει 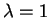 και
και 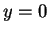 .
Άρα κάθε
ιδιοδιάνυσμα είναι της μορφής
.
Άρα κάθε
ιδιοδιάνυσμα είναι της μορφής 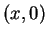 .
Κατα συνέπεια ο υπόχωρος
που παράγεται από τα ιδιοδιανύσματα είναι μονοδιάστατος και φυσικά
το
.
Κατα συνέπεια ο υπόχωρος
που παράγεται από τα ιδιοδιανύσματα είναι μονοδιάστατος και φυσικά
το 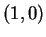 είναι μια βάση του χώρου αυτού.
είναι μια βάση του χώρου αυτού.
Vassilis Metaftsis
1999-09-15