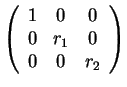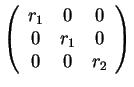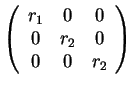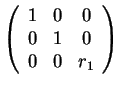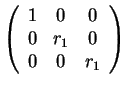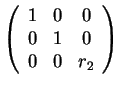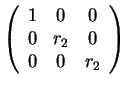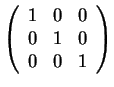Next: Άσκηση 31
Up: Άσκηση 30
Previous: Υπόδειξη
Εφόσον ο πίνακας  ικανοποιεί την σχέση
ικανοποιεί την σχέση 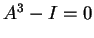 έχουμε ότι το
ελάχιστο πολυώνυμο του
έχουμε ότι το
ελάχιστο πολυώνυμο του  διαιρεί το πολυώνυμο
διαιρεί το πολυώνυμο
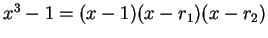 όπου
όπου
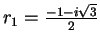 και
και
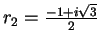 .
Άρα οι πιθανοί στοιχειώδεις
διαιρέτες του πίνακα είναι οι παρακατω
.
Άρα οι πιθανοί στοιχειώδεις
διαιρέτες του πίνακα είναι οι παρακατω
- .
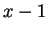 ,
,
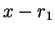 ,
,
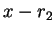
- .
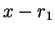 ,
,
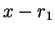 ,
,
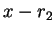
- .
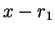 ,
,
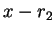 ,
,
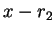
- .
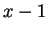 ,
,
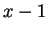 ,
,
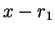
- .
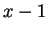 ,
,
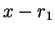 ,
,
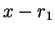
- .
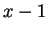 ,
,
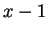 ,
,
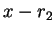
- .
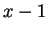 ,
,
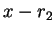 ,
,
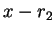
- .
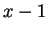 ,
,
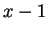 ,
,
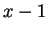
- .
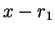 ,
,
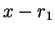 ,
,
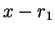
- .
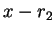 ,
,
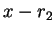 ,
,
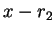
Άρα οι πιθανές μορφές Jordan είναι οι εξής
- .
-
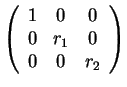
- .
-
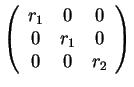
- .
-
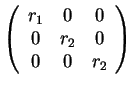
- .
-
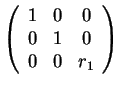
- .
-
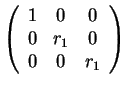
- .
-
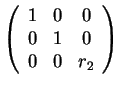
- .
-
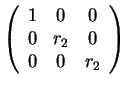
- .
-
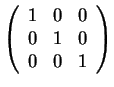
- .
-
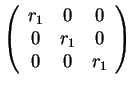
- .
-
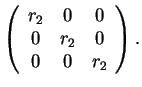
Vassilis Metaftsis
1999-09-15