


Next: Άσκηση 41
Up: Άσκηση 40
Previous: Υπόδειξη
Aν 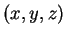 είναι ένα στοιχείο του
είναι ένα στοιχείο του 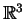 τότε ο πυρήνας της
τότε ο πυρήνας της
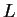 αποτελείται από τα στοιχεία για τα οποία ισχύει
αποτελείται από τα στοιχεία για τα οποία ισχύει
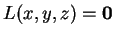 ή
ισοδύναμα
ή
ισοδύναμα 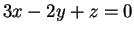 .
Άρα, ο πυρήνας αποτελείται από τις λύσεις της
παραπάνω εξίσωσης, και προφανώς είναι υπόχωρος του
.
Άρα, ο πυρήνας αποτελείται από τις λύσεις της
παραπάνω εξίσωσης, και προφανώς είναι υπόχωρος του 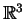 διάστασης 2.
Από την άλλη, εφόσον το
διάστασης 2.
Από την άλλη, εφόσον το 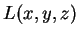 δεν είναι πάντα μηδέν, η εικόνα
της
δεν είναι πάντα μηδέν, η εικόνα
της 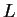 είναι ολόκληρο το
είναι ολόκληρο το 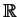 (διάστασης 1).
(διάστασης 1).
Vassilis Metaftsis
1999-09-15