


Next: Άσκηση 43
Up: Άσκηση 42
Previous: Υπόδειξη
Υποθέτω ότι η dim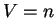 και η dim(Im
και η dim(Im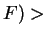 dim
dim .
Τότε υπάρχουν διανύσματα
.
Τότε υπάρχουν διανύσματα
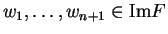 τα
οποία είναι γραμμικώς ανεξάρτητα. Έστω
τα
οποία είναι γραμμικώς ανεξάρτητα. Έστω
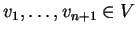 ώστε
ώστε 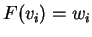 .
Έστω
.
Έστω
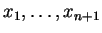 στοιχεία του σώματος
στοιχεία του σώματος
 ώστε
ώστε
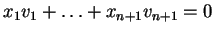 .
Τότε
.
Τότε
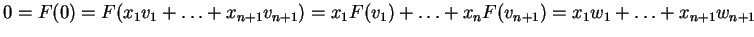 .
Όμως, η γραμμική ανεξαρτησία των
.
Όμως, η γραμμική ανεξαρτησία των
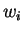 συνεπάγεται ότι
συνεπάγεται ότι
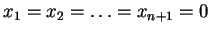 και άρα τα
στοιχεία
και άρα τα
στοιχεία
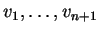 είναι γραμμικώς ανεξάρτητα, άτοπο
μιας και η διάσταση του
είναι γραμμικώς ανεξάρτητα, άτοπο
μιας και η διάσταση του  είναι
είναι 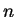 .
Άρα
dim(Im
.
Άρα
dim(Im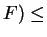 dim
dim .
.
Vassilis Metaftsis
1999-09-15