


Next: Άσκηση 44
Up: Άσκηση 43
Previous: Υπόδειξη
Θεωρούμε την συνήθη βάση του 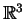 ,
,
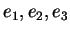 .
Eφόσον τα
διανύσματα
.
Eφόσον τα
διανύσματα 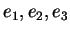 είναι γραμμικώς ανεξάρτητα από Θεώρημα
18 υπάρχει μοναδική απεικόνιση
είναι γραμμικώς ανεξάρτητα από Θεώρημα
18 υπάρχει μοναδική απεικόνιση  ώστε
ώστε
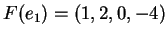 ,
,
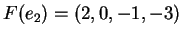 και
και
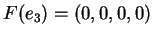 .
Επιπλέον, η Im
.
Επιπλέον, η Im παράγεται από τα διανύσματα που μας
δίνονται αφού κάθε στοιχείο του
παράγεται από τα διανύσματα που μας
δίνονται αφού κάθε στοιχείο του 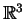 παράγεται από τα
παράγεται από τα
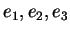 .
Άρα η παραπάνω είναι η ζητούμενη γραμμική
απεικόνιση. Ο γενικός τύπος της
.
Άρα η παραπάνω είναι η ζητούμενη γραμμική
απεικόνιση. Ο γενικός τύπος της  δίνεται από την
δίνεται από την
Vassilis Metaftsis
1999-09-15