


Next: Άσκηση 46
Up: Άσκηση 45
Previous: Υπόδειξη
Αφού η  είναι μηδενοδύναμη, η
είναι μηδενοδύναμη, η 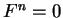 .
Άρα ισχύει η ταυτότητα
.
Άρα ισχύει η ταυτότητα
Oι απεικονίσεις
και
είναι
γραμμικές, σαν σύνθεση γραμμικών απεικονίσεων. Η παραπάνω εξίσωση
γίνεται
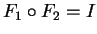 και ξέρω ότι η
και ξέρω ότι η 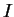 είναι 1-1 και επί. Άρα
και η
είναι 1-1 και επί. Άρα
και η 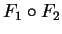 είναι 1-1 και επί άρα η
είναι 1-1 και επί άρα η 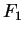 είναι 1-1 και η
είναι 1-1 και η
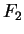 είναι επί. Όμως και οι δύο απεικονίσεις
είναι επί. Όμως και οι δύο απεικονίσεις 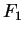 και
και 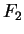 είναι ορισμένες από το
είναι ορισμένες από το  στο
στο  και άρα είναι 1-1 και επί.
και άρα είναι 1-1 και επί.
Vassilis Metaftsis
1999-09-15