


Next: Άσκηση 47
Up: Άσκηση 46
Previous: Υπόδειξη
Υπολογίζω τον πυρήνα της  .
Αν
.
Αν 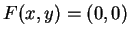 τότε
τότε
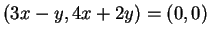 και το σύστημα που προκύπτει δίνει
και το σύστημα που προκύπτει δίνει 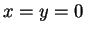 .
Άρα ο πυρήνας της
.
Άρα ο πυρήνας της  είναι
τετριμμένος και άρα η
είναι
τετριμμένος και άρα η  είναι 1-1. Επομένως, η εικόνα της
είναι 1-1. Επομένως, η εικόνα της  έχει διάσταση
δύο και άρα είναι ισομορφική με το
έχει διάσταση
δύο και άρα είναι ισομορφική με το 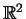 .
Άρα από Θεώρημα 21
η
.
Άρα από Θεώρημα 21
η  είναι 1-1 και επί και άρα είναι αντιστρέψιμη.
είναι 1-1 και επί και άρα είναι αντιστρέψιμη.
Vassilis Metaftsis
1999-09-15