


Next: Άσκηση 49
Up: Γραμμικές Απεικονίσεις και Πίνακες
Previous: Γραμμικές Απεικονίσεις και Πίνακες
Ορισμός 26
Έστω
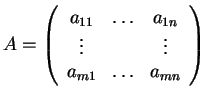
ένας
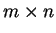
πίνακας με στοιχεία στο σώμα

.
Η γραμμική απεικόνιση που αντιστοιχεί στον

είναι η
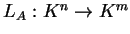
με
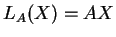
για κάθε
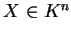
.
Η
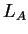
είναι γραμμική απεικόνιση.
Θεώρημα 25
Αν
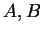
είναι
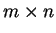
πίνακες και
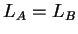
τότε
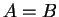
.
Με άλλα λόγια
αν οι απεικονίσεις που αντιστοιχούν στους πίνακες
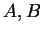
είναι ίσες τότε
και οι πίνακες είναι ίσοι.
Θεώρημα 26
Αν
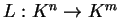
είναι μια γραμμική απεικόνιση τότε υπάρχει μοναδικός
πίνακας

ώστε
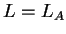
.
Θεώρημα 27
Έστω

είναι ένας
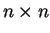
πίνακας και
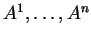
οι στήλες του

.
Τότε ο

είναι αντιστρέψιμος αν και μόνο αν τα
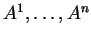
είναι γραμμικώς ανεξάρτητα στοιχεία.
Θεώρημα 28
Έστω
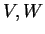
διανυσματικοί χώροι με βάσεις
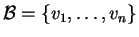
και
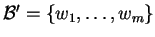
αντίστοιχα. Aν
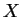
είναι το
διάνυσμα συντεταγμένων ενός στοιχείου

ως προς την βαση
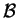
τότε υπάρχει μια μοναδική γραμμική απεικόνιση
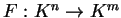
με πίνακα

τέτοια ώστε το
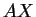
να είναι το διάνυσμα
συντεταγμένων του
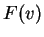
ως προς την βάση
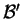
.
O πίνακας

συμβολίζεται με
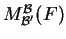
ενώ τα αντίστοιχα διανύσματα
συνταταγμένων συμβολίζονται με
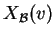
.
Θεώρημα 29
Έστω
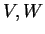
διανυσματικοί χώροι και
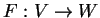
γραμμική απεικόνιση. Έστω
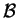
μια βάση του

και
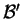
μια βάση του

.
Aν

τότε
Θεώρημα 30
Έστω
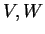
διανυσματικοί χώροι,
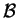
βάση του

και
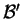
βάση του

.
Έστω
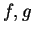
γραμμικές απεικονίσεις από το

στο

.
Αν
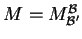
τότε
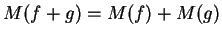
.
Επιπλέον, αν

τότε
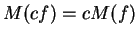
.
Η απεικόνιση
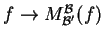
είναι ισομορφισμός μεταξύ του
χώρου των γραμμικών απεικονίσεων
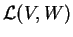
και του χώρου
των
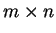
πινάκων (
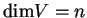
,
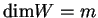
).
Θεώρημα 31
Έστω
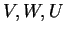
διανυσματικοί χώροι. Έστω
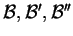
βάσεις των
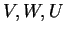
αντίστοιχα. Aν
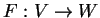
και
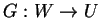
γραμμικές απεικονίσεις τότε
Ορισμός 27
Αν
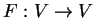
γραμμική απεικόνιση και
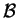
βάση του

,
ο πίνακας
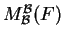
καλείται ο πίνακας της

ως προς
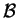
.
Πόρισμα 10
Αν

διανυσματικός χώρος και
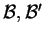
βάσεις του

τότε
Ειδικότερα, ο πίνακας
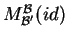
είναι αντιστρέψιμος.
Θεώρημα 32
Έστω
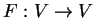
γραμμική απεικόνιση και
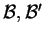
βάσεις του

.
Τότε υπάρχει αντιστρέψιμος πίνακας
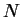
τέτοιος ώστε
Eιδικότερα, μπορούμε
να πάρουμε
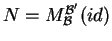
.
Ορισμός 28
Δύο πίνακες
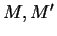
λέγονται όμοιοι αν υπάρχει αντιστρέψιμος πίνακας
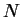
ώστε
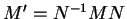
.
Vassilis Metaftsis
1999-09-15
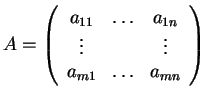 ένας
ένας 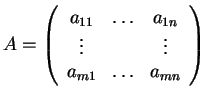 ένας
ένας