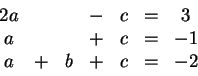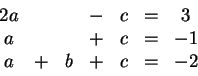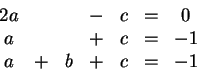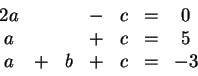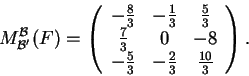Next: Άσκηση 52
Up: Άσκηση 51
Previous: Υπόδειξη
Το
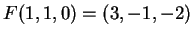 .
Έστω
.
Έστω
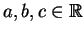 ώστε
ώστε
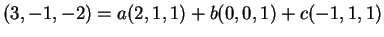 .
Το σύστημα που προκύπτει δίνει
.
Το σύστημα που προκύπτει δίνει
το οποίο δίνει
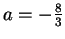 ,
,
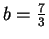 και
και
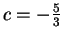 .
Το
.
Το
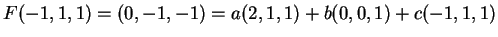 .
Το σύστημα που προκύπτει είναι
.
Το σύστημα που προκύπτει είναι
το οποίο δίνει
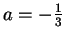 ,
,
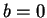 και
και
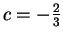 .
Τέλος, το
.
Τέλος, το
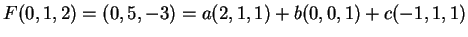 .
Το σύστημα που προκύπτει είναι
.
Το σύστημα που προκύπτει είναι
οι λύσεις του οποίου είναι 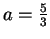 ,
,
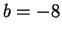 και
και
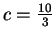 .
Άρα
.
Άρα
Vassilis Metaftsis
1999-09-15