


Next: Υπόδειξη
Up: Εσωτερικά Γινόμενα, Καθετότητα
Previous: Λύση
Έστω  διανυσματικός χώρος με εσωτερικό γινόμενο. Oρίζουμε γωνία
διανυσματικός χώρος με εσωτερικό γινόμενο. Oρίζουμε γωνία
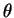 μεταξύ δύο διανυσμάτων
μεταξύ δύο διανυσμάτων 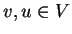 την μοναδική γωνία
την μοναδική γωνία
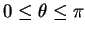 τέτοια ώστε
τέτοια ώστε
Έστω  ο διανυσματικός χώρος των πραγματικών συναρτήσεων στο διάστημα
ο διανυσματικός χώρος των πραγματικών συναρτήσεων στο διάστημα
![$[0,1]$](img840.gif) με εσωτερικό γινόμενο το
με εσωτερικό γινόμενο το
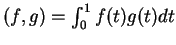 .
Βρείτε
το
.
Βρείτε
το 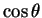 για την γωνία
για την γωνία 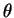 μεταξύ των διανυσμάτων
μεταξύ των διανυσμάτων 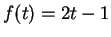 και
και
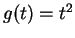 .
.
Vassilis Metaftsis
1999-09-15
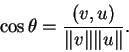
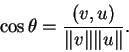
![]() ο διανυσματικός χώρος των πραγματικών συναρτήσεων στο διάστημα
ο διανυσματικός χώρος των πραγματικών συναρτήσεων στο διάστημα
![]() με εσωτερικό γινόμενο το
με εσωτερικό γινόμενο το
![]() .
Βρείτε
το
.
Βρείτε
το ![]() για την γωνία
για την γωνία ![]() μεταξύ των διανυσμάτων
μεταξύ των διανυσμάτων ![]() και
και
![]() .
.