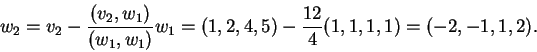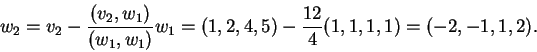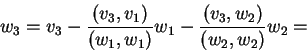Next: Άσκηση 65
Up: Άσκηση 64
Previous: Υπόδειξη
Θέτω
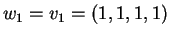 .
Τότε,
.
Τότε,
Για
να αποφύγουμε πράξεις με κλάσματα, αντικαθιστούμε το 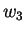 με το
με το
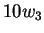 και παίρνουμε
και παίρνουμε
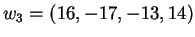 .
Τα
.
Τα 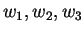 αποτελούν ορθογώνια βάση του υπόχωρου. Για να κανονικοποιήσουμε
την βάση βρίσκουμε
αποτελούν ορθογώνια βάση του υπόχωρου. Για να κανονικοποιήσουμε
την βάση βρίσκουμε 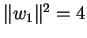 ,
,
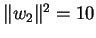 και
και
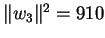 .
Άρα τα παρακάτω διανύσματα είναι μια ορθοκανονική
βάση του υπόχωρου:
.
Άρα τα παρακάτω διανύσματα είναι μια ορθοκανονική
βάση του υπόχωρου:
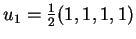 ,
,
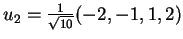 και
και
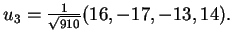
Vassilis Metaftsis
1999-09-15