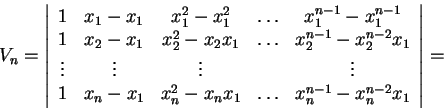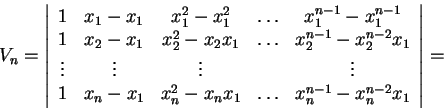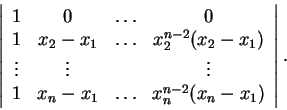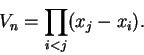Next: About this document ...
Up: Άσκηση 75
Previous: Υπόδειξη
Έστω 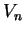 η αρχική ορίζουσα. Πολλαπλασιάζω κάθε στήλη με
η αρχική ορίζουσα. Πολλαπλασιάζω κάθε στήλη με 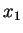 και αφαιρώ από την επόμενη, αρχίζοντας από την δεύτερη από δεξιά.
Έτσι παίρνω
και αφαιρώ από την επόμενη, αρχίζοντας από την δεύτερη από δεξιά.
Έτσι παίρνω
Αναπτύσσω ως προς την γραμμή 1 και παίρνω:
Συνεχίζοντας με τον ίδιο τρόπο παίρνουμε τελικά ότι
Vassilis Metaftsis
1999-09-15