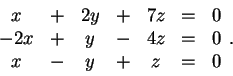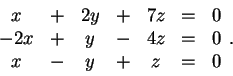Next: Άσκηση 12
Up: Άσκηση 11
Previous: Υπόδειξη
Το σύστημα
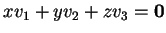 δίνει
δίνει
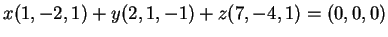 ή ισοδύναμα
ή ισοδύναμα
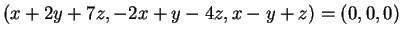 .
Άρα
.
Άρα
Λύνοντας την τρίτη εξίσωση ως προς 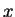 και αντικαθιστώντας
στις άλλες δύο βρίσκω
και αντικαθιστώντας
στις άλλες δύο βρίσκω 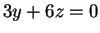 και
και 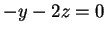 .
Εφόσον οι δύο εξισώσεις
είναι ισοδύναμες, το σύστημα έχει και μη-μηδενική λύση, άρα τα
διανύσματα είναι γραμμικώς εξαρτημένα.
.
Εφόσον οι δύο εξισώσεις
είναι ισοδύναμες, το σύστημα έχει και μη-μηδενική λύση, άρα τα
διανύσματα είναι γραμμικώς εξαρτημένα.
Vassilis Metaftsis
1999-09-15