


Next: Άσκηση 13
Up: Άσκηση 12
Previous: Υπόδειξη
Υποθέτω ότι
όπου 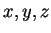 στοιχεία
του σώματος. Τότε
στοιχεία
του σώματος. Τότε
. Αλλά ξέρουμε ότι
τα 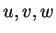 είναι γραμμικώς ανεξάρτητα, άρα στην παραπάνω εξίσωση
οι συντελεστές των
είναι γραμμικώς ανεξάρτητα, άρα στην παραπάνω εξίσωση
οι συντελεστές των 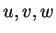 είναι μηδέν. Άρα
είναι μηδέν. Άρα 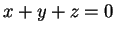 ,
,
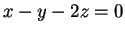 και
και 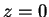 .
Xρησιμοποιώντας την τρίτη εξίσωση λύνουμε τις δύο
πρώτες και βρίσκουμε
.
Xρησιμοποιώντας την τρίτη εξίσωση λύνουμε τις δύο
πρώτες και βρίσκουμε 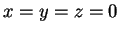 .
Άρα τα
.
Άρα τα
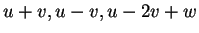 είναι
γραμμικώς ανεξάρτητα.
είναι
γραμμικώς ανεξάρτητα.
Vassilis Metaftsis
1999-09-15