


Next: Άσκηση 16
Up: Άσκηση 15
Previous: Υπόδειξη
Έστω
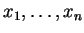 στοιχεία του σώματος τέτοια ώστε
στοιχεία του σώματος τέτοια ώστε
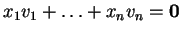 .
Πολλαπλασιάζω την παραπάνω εξίσωση με
.
Πολλαπλασιάζω την παραπάνω εξίσωση με
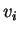 για κάθε
για κάθε 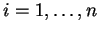 και παίρνω
και παίρνω
. Aπό την πρώτη εξίσωση έχω
Eπειδή τα
διανύσμτα είναι κάθετα αν δύο έχω ότι
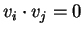 για κάθε
για κάθε
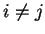 .
Άρα η πρώτη εξίσωση δίνει
.
Άρα η πρώτη εξίσωση δίνει
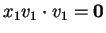 και
εφόσον το
και
εφόσον το 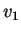 είναι μη-μηδενικό έχω ότι
είναι μη-μηδενικό έχω ότι 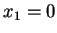 .
Όμοια, αν
εξετάσω τις υπόλοιπες εξισώσεις παίρνω ότι
.
Όμοια, αν
εξετάσω τις υπόλοιπες εξισώσεις παίρνω ότι 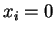 για κάθε
για κάθε
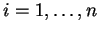 .
Άρα τα
.
Άρα τα
 γραμμικώς ανεξάρτητα.
γραμμικώς ανεξάρτητα.
Vassilis Metaftsis
1999-09-15