


Next: Άσκηση 21
Up: Άσκηση 20
Previous: Υπόδειξη
Αν 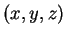 είναι ένα τυχαίο στοιχείο του
είναι ένα τυχαίο στοιχείο του  ,
υποθέτω ότι
υπάρχουν
,
υποθέτω ότι
υπάρχουν
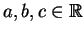 ώστε
ώστε
To παραπάνω
σύστημα δίνει 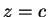 ,
,
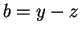 και
και 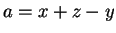 .
Aν τώρα
.
Aν τώρα
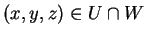 τότε υπάρχουν πραγματικοί αριθμοί
τότε υπάρχουν πραγματικοί αριθμοί 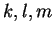 ώστε
ώστε
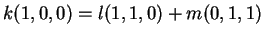 ή ισοδύναμα
ή ισοδύναμα
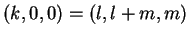 από
το οποίο παίρνουμε
από
το οποίο παίρνουμε 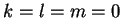 .
Άρα
.
Άρα
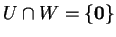 και τελικά
και τελικά
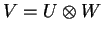 .
.
Vassilis Metaftsis
1999-09-15