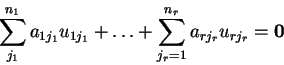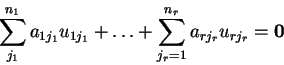Next: Άσκηση 24
Up: Άσκηση 23
Previous: Υπόδειξη
Υποθέτω ότι
όπου τα 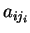 στοιχεία του σώματος. Κάθε
στοιχεία του σώματος. Κάθε
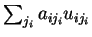 ανήκει στο
ανήκει στο 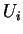 .
Eφόσον το
.
Eφόσον το  είναι το ευθύ άθροισμα των
είναι το ευθύ άθροισμα των 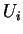 το
μόνο κοινό στοιχείο των
το
μόνο κοινό στοιχείο των 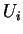 είναι το
είναι το 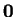 και άρα
και άρα
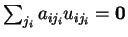 για κάθε
για κάθε 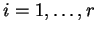 .
Αλλά τα στοιχεία
των
.
Αλλά τα στοιχεία
των 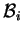 είναι γραμμικώς ανεξάρτητα επομένως τα
είναι γραμμικώς ανεξάρτητα επομένως τα 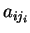 είναι
μηδέν για κάθε
είναι
μηδέν για κάθε 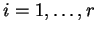 .
Mε άλλα λόγια το
.
Mε άλλα λόγια το 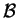 αποτελείται
από γραμμικά ανεξάρτητα στοιχεία.
αποτελείται
από γραμμικά ανεξάρτητα στοιχεία.
Vassilis Metaftsis
1999-09-15