


Next: Άσκηση 25
Up: Άσκηση 24
Previous: Υπόδειξη
Αρχικά βλέπω ότι
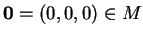 .
Επιπλέον, αν
.
Επιπλέον, αν
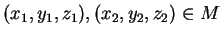 τότε
τότε 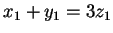 και
και
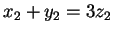 .
Συνεπώς,
.
Συνεπώς,
με
Τέλος, αν 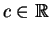 τότε
τότε
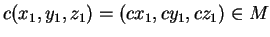 γιατί
γιατί
Άρα ο 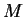 είναι
διανυσματικός υπόχωρος του
είναι
διανυσματικός υπόχωρος του 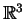 .
.
Eύκολα βλέπω ότι
Άρα τα σύνολα
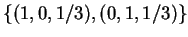 και
και
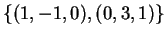 αποτελούν
βάσεις του
αποτελούν
βάσεις του 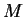 .
Θεωρώ
.
Θεωρώ 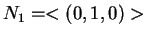 τον υπόχωρο του
τον υπόχωρο του 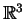 που
παράγεται από το στοιχείο
που
παράγεται από το στοιχείο 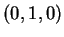 και
και 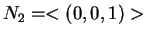 τον
υπόχωρος που παράγεται από το
τον
υπόχωρος που παράγεται από το 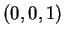 .
Είναι φανερό ότι
.
Είναι φανερό ότι 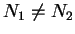 .
Θα δείξω πρώτα ότι
.
Θα δείξω πρώτα ότι
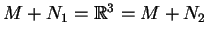 .
Πράγματι, αν
.
Πράγματι, αν
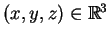 τότε
τότε
και
και στις δύο
περιπτώσεις το 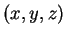 γράφετε σαν γραμμικός συνδυασμός
στοιχείων μιας βάσης του
γράφετε σαν γραμμικός συνδυασμός
στοιχείων μιας βάσης του 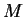 και μιας βάσης του
και μιας βάσης του 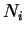 ,
,
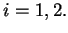 Θα
δείξω τώρα ότι
Θα
δείξω τώρα ότι
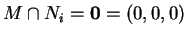 για κάθε
για κάθε 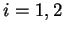 .
Αν
.
Αν
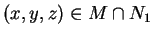 τότε
τότε
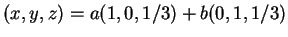 και
και
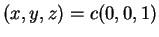 .
Το πρώτο σύστημα δίνει
.
Το πρώτο σύστημα δίνει 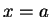 ,
,
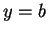 ,
,
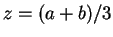 και το δεύτερο
και το δεύτερο 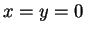 ,
,
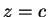 από το οποίο παίρνω
από το οποίο παίρνω
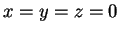 .
Αν τώρα
.
Αν τώρα
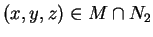 τότε
τότε
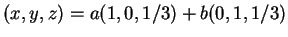 και
και
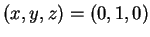 .
Το πρώτο
σύστημα δίνει
.
Το πρώτο
σύστημα δίνει 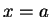 ,
,
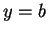 ,
,
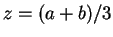 και το δεύτερο
και το δεύτερο 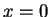 ,
,
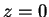 ,
, 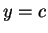 από τα οποία συνάγω ότι
από τα οποία συνάγω ότι 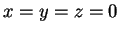 .
Άρα
.
Άρα
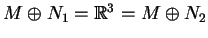 .
.
Vassilis Metaftsis
1999-09-15