


Next: Γραμμικά Συστήματα και Πίνακες
Up: Άσκηση 25
Previous: Υπόδειξη
Αν τα
 είναι γραμμικώς ανεξάρτητα τότε θεωρώ το τυχαίο
στοιχείο
είναι γραμμικώς ανεξάρτητα τότε θεωρώ το τυχαίο
στοιχείο
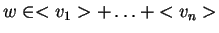 .
Το
.
Το 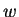 γράφεται σαν
γράφεται σαν
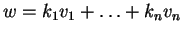 .Αν τώρα
.Αν τώρα 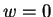 τότε η γραμμική ανεξαρτησία
συνεπάγεται ότι
τότε η γραμμική ανεξαρτησία
συνεπάγεται ότι 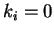 για κάθε
για κάθε 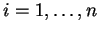 και συνεπώς
και συνεπώς
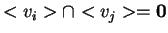 για κάθε
για κάθε 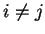 .
Άρα το άθροισμα είναι ευθύ.
.
Άρα το άθροισμα είναι ευθύ.
Αντίστροφα, αν το άθροισμα είναι ευθύ, το
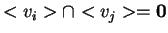 για κάθε
για κάθε
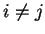 ,
επομένως ένας γραμμικώς συνδυασμός της μορφής
,
επομένως ένας γραμμικώς συνδυασμός της μορφής
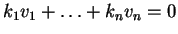 συνεπάγεται ότι
συνεπάγεται ότι 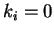 για κάθε
για κάθε 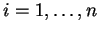 και άρα τα
και άρα τα
 είναι γραμμικώς ανεξάρτητα.
είναι γραμμικώς ανεξάρτητα.
Vassilis Metaftsis
1999-09-15
![]() για κάθε
για κάθε
![]() ,
επομένως ένας γραμμικώς συνδυασμός της μορφής
,
επομένως ένας γραμμικώς συνδυασμός της μορφής
![]() συνεπάγεται ότι
συνεπάγεται ότι ![]() για κάθε
για κάθε ![]() και άρα τα
και άρα τα
![]() είναι γραμμικώς ανεξάρτητα.
είναι γραμμικώς ανεξάρτητα.