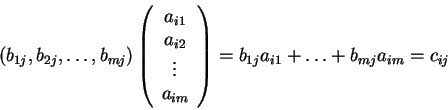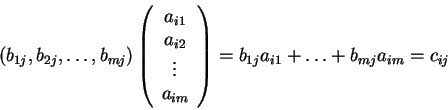Next: Άσκηση 27
Up: Άσκηση 26
Previous: Υπόδειξη
- .
- Αν
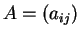 και
και 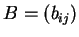 τότε το
τότε το 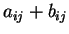 είναι
το
είναι
το 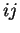 στοιχείο του
στοιχείο του 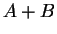 .
Άρα το
.
Άρα το 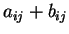 είναι το
είναι το 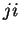 στοιχείο
του πίνακα
στοιχείο
του πίνακα 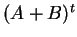 .
Από την άλλη, το
.
Από την άλλη, το 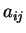 είναι το
είναι το 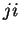 στοιχείο
του
στοιχείο
του 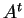 και το
και το 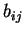 είναι το
είναι το 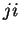 στοιχείο του
στοιχείο του 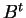 άρα το
άρα το
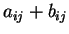 είναι το
είναι το 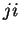 στοιχείο του
στοιχείο του 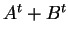 .
Επομένως,
.
Επομένως,
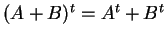 .
.
- .
- Προφανώς, διπλή αλλαγή των γραμμών με τις στήλες ενός πίνακα
δεν επιφέρει καμία αλλαγή στον τελικό πίνακα.
- .
- Το
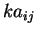 είναι το
είναι το 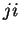 στοιχείο του πίνακα
στοιχείο του πίνακα 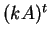 .
Όμως,
αν
.
Όμως,
αν 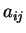 είναι το
είναι το 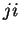 στοιχείο του
στοιχείο του 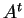 τότε το
τότε το 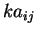 είναι
το
είναι
το 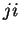 στοιχείο του
στοιχείο του 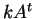 .
Tελικά,
.
Tελικά, 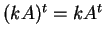 .
.
- .
- Το
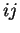 στοιχείο του
στοιχείο του 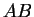 είναι το στοιχείο
είναι το στοιχείο
Άρα, το 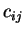 είναι το
είναι το 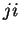 στοιχείο του
στοιχείο του 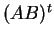 .
Όμως, το
.
Όμως, το 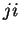 στοιχείο
του
στοιχείο
του 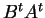 είναι το στοιχείο που προκύπτει από την
είναι το στοιχείο που προκύπτει από την 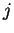 στήλη του
στήλη του 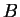 (που
γίνεται
(που
γίνεται 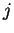 γραμμή στον
γραμμή στον 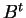 )
επί την
)
επί την 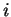 γραμμή του
γραμμή του  (που γίνεται
(που γίνεται
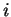 στήλη στον
στήλη στον 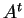 ). Δηλαδή το
). Δηλαδή το 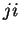 στοιχείο του
στοιχείο του 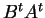 είναι
το
είναι
το
και άρα
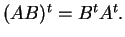
Vassilis Metaftsis
1999-09-15