Για να ορίσουμε επακριβώς την τυχαιότητα στη ρίψη της βελόνας, θεωρούμε ότι το μέσο της βελόνας πέφτει τυχαία στο διάστημα μήκους 2α, που είναι η απόσταση που χωρίζει τις γειτονικές παράλληλες ευθείες του επιπέδου και η γωνία φ μεταξύ των παραλλήλων ευθειών και της βελόνας είναι ομοιόμορφα κατανεμημένη στο διάστημα και ανεξάρτητη από την απόσταση από την κοντινότερη παράλληλο, που την συμβολίζουμε με x. Έτσι, το αποτέλεσμα της ρίψης δίνεται από το ζευγάρι (φ,x), που κείτεται σε ένα ορθογώνιο παραλληλόγραμμο με πλευρές π και α (βλ. σχήμα 6).

Από το σχήμα 5 φαίνεται ότι η βελόνα τέμνει την παράλληλη τότε και μόνο τότε όταν x<lημφ.

Έτσι η ζητούμενη πιθανότητα ισούται με το λόγο του εμβαδού της γραμμοσκιασμένης περιοχής Α προς το εμβαδόν του παραλληλογράμμου:

P(A)= 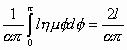.