Έστω Ω ο χώρος των στοιχειωδών ενδεχομένων, που τον ονομάζουμε δειγματικό χώρο. Ενδεχόμενο Α ονομάζεται οποιοδήποτε στοιχείο μιας κλάσης υποσυνόλων του Ω, που σχηματίζουν σ- άλγεβρα και την συμβολίζουμε με Β. Πιθανότητα P(A) ονομάζεται μια συνάρτηση που ορίζεται πάνω στην σ- άλγεβρα Β και παίρνει τιμές στο διάστημα [0, 1]. Η τριάδα (Ω, Β, Ρ) ονομάζεται πιθανοθεωρητικός χώρος.

Όταν ο δειγματικός χώρος Ω περιέχει πεπερασμένο πλήθος ισοπίθανων στοιχειωδών ενδεχομένων έχουμε το κλασικό σχήμα πιθανοτήτων. Εάν n είναι ο αριθμός των δυνατών στοιχειωδών ενδεχομένων και m ο αριθμός των ευνοϊκών για το ενδεχόμενο Α, τότε

Ρ(Α) = .

Έστω κ ομάδες αντικειμένων, όπου η i ομάδα αποτελείται από n_i αντικείμενα. Διαλέγουμε ένα αντικείμενο από κάθε ομάδα. Τότε ο συνολικός αριθμός Ν των τρόπων με τους οποίους μπορεί να γίνει η διαλογή δίνεται από την σχέση:

Ν= n₁· n₂··· n_κ

Το πλήθος των μεταθέσεων n αντικειμένων δίνεται από τον τύπο:

P_n = n!

Το πλήθος των διατάξεων m αντικειμένων από n δίνεται από τον τύπο:

(n)_m =n(n-1)···(n-m+1) =

Το πλήθος των συνδυασμών m αντικειμένων από n δίνεται από τον τύπο:

= =

Έστω n= n₁+n₂+…+n_k διαφορετικά αντικείμενα, με n₁ από αυτά πρώτου τύπου,…, nk από αυτά κ- τύπου. Επιλέγω τυχαία m= m₁+ m₂+…+ mk αντικείμενα. Η πιθανότητα να βγάλω m₂ (n₂) του δευτέρου τύπου,…, m_k ( n_k) του κ- τύπου, δίνει την υπεργεωμετρική κατανομή με τον τύπο:

P(A)= P(m₁, …, m_k)=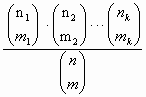

Έστω ο δειγματικός χώρος παριστά κάποια περιοχή Ω με μέτρο μ(Ω), όπως μήκος, εμβαδόν, όγκος, κ.τ.λ. (0<μ(Ω)<). Λέμε ότι ένα σημείο πέφτει ομοιόμορφα στην περιοχή Ω εάν η πιθανότητα να βρεθεί σε κάποια περιοχή Α, υποπεριοχή του Ω, είναι ανάλογη του μέτρου μ(Α):

P(A)=.

Υπόδειξη άσκησης

Υπόδειξη άσκησης

Υπόδειξη άσκησης

Υπόδειξη άσκησης

Βρείτε την πιθανότητα στο Λόττο, με 6 επιλογές από 49 αριθμούς, να πετύχουμε 3 νούμερα ( ενδεχόμενο Α₃), 4 νούμερα (ενδεχόμενο Α₄), 5 νούμερα (ενδεχόμενο Α₅), 6 νούμερα (ενδεχόμενο Α₆).

Έστω n όμοια αντικείμενα τοποθετούνται σε m κελιά. Διαφορετικές τοποθετήσεις θεωρούνται αυτές με διαφορετικό αριθμό αντικειμένων σε κάθε κελί. Βρείτε την πιθανότητα να βρεθούν σε συγκεκριμένο κελί κ αντικείμενα.

Έστω n όμοια αντικείμενα τοποθετούνται σε m κελιά με mn και κάθε κελί χωράει μόνο ένα αντικείμενο. Βρείτε την πιθανότητα να βρεθούν κατειλημμένα κ συγκεκριμένα κελιά (κn).

Λύση άσκησης

Σε κύκλο ακτίνας R=1 ρίχνουμε τυχαία ένα σημείο. Να βρεθεί η πιθανότητα να βρεθεί το σημείο πάνω σε κύκλο με ακτίνα r = ½, με το ίδιο κέντρο.

Υπόδειξη άσκησης

Έστω ότι η εμφάνιση σε δέκτη καθενός από τα 2 σήματα που εκπέμπονται είναι εξίσου δυνατή σε οποιαδήποτε στιγμή κατά τη διάρκεια ενός χρονικού διαστήματος μήκους Τ. Βρείτε την πιθανότητα το χρονικό διάστημα μεταξύ των εμφανίσεων των 2 σημάτων να είναι μικρότερο του τ, (τ<Τ).

Έστω επίπεδο με παράλληλες ευθείες με απόσταση μεταξύ τους 2α. Στο επίπεδο ρίχνουμε τυχαία βελόνα μήκους 2l (l<α). Βρείτε την πιθανότητα η βελόνα να τέμνει ευθεία του επιπέδου (βλ. σχήμα 5).

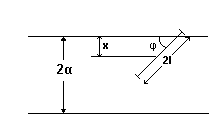
 Σχήμα 5

Περιεχόμενα