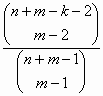Λύση Άσκησης 8
Ας βρούμε το πλήθος όλων
των δυνατών τοποθετήσεων. Θεωρούμε στη
σειρά n+m-1 άσπρα
σφαιρίδια (σχήμα 1) και επιλέγουμε τυχαία m-1
από αυτά
Σχήμα 1
που τα μαυρίζουμε. Τα άσπρα
αντιστοιχούν στα αντικείμενα του
προβλήματος και τα μαύρα στα τοιχώματα των
m
κελιών. Δεν είναι δύσκολο να
δούμε μια αμφιμονοσήμαντη αντιστοιχία
μεταξύ της τυχαίας επιλογής των
αντικειμένων στα κελιά. Έτσι στο παραπάνω
σχήμα δείχνεται στο πρώτο κελί να
τοποθετείται ένα αντικείμενο, στο δεύτερο 3
αντικείμενα κ.τ.λ. Ο συνολικός
αριθμός των διαφορετικών τοποθετήσεων
δίνεται με το συνδυασμό
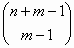 .
.
Έστω τώρα σε ένα
συγκεκριμένο κελί έχουμε κ αντικείμενα.
Τότε τα υπόλοιπα n-κ
αντικείμενα θα πρέπει να τοποθετηθούν στα
άλλα m-1 κελιά. Αυτό
μπορεί να γίνει με 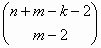 τρόπους, σύμφωνα με τα
προηγούμενα. Έτσι η ζητούμενη πιθανότητα
είναι: P(A)=
τρόπους, σύμφωνα με τα
προηγούμενα. Έτσι η ζητούμενη πιθανότητα
είναι: P(A)=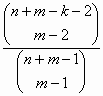
Εκφώνηση
άσκησης
Υπόδειξη άσκησης
Περιεχόμενα